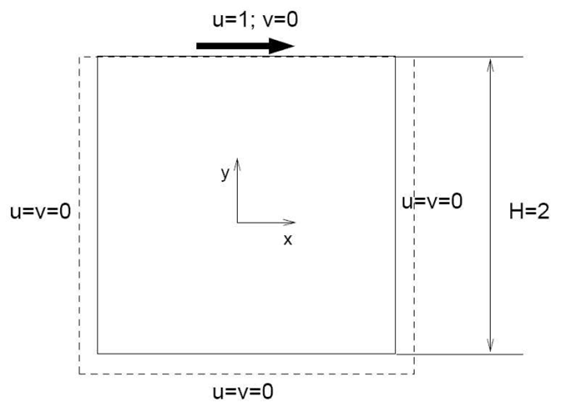
Fig. 1 Schematic of 2D lid-driven cavity flow
Keywords
shear-driven flow, laminar flow, incompressible flow, viscous flow
Purposes
• Validation of GASFLOW for laminar viscous flow with Mach number at nearly zero.
Descriptions
• The lid-driven cavity is an important fluid mechanical system serving as a benchmark for testing numerical methods and for studying fundamental aspects of incompressible flows in confined volumes which are driven by the tangential motion of a bounding wall.
• Lid-driven cavity flow retains a rich fluid flow physics manifested by multiple counter rotating recirculating regions on the corners of the cavity depending on the Reynolds number.
• A square cavity with a height H = 2 m (Fig. 1) has been set up. The top wall moves with the velocity of 1 m/s in X direction. The bottom and side walls are no-slip and stationary. The Reynolds number of the flow is 1000.
• A locally refined mesh with 80*80 in X and Y axes (Fig. 2).

Fig. 1 Schematic of 2D lid-driven cavity flow
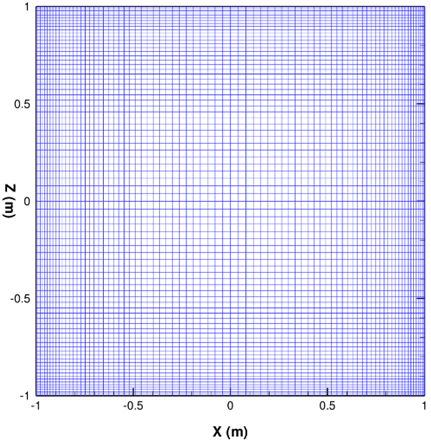
Fig. 2 GASFLOW computing grid
Results
• The velocity and streamline calculated by GASFLOW are illustrated in Figs. 3~6.
• The center-line velocities using the first-order upwind and second-order Van Leer schemes in GASFLOW were compared with the data, as shown in Fig. 7.
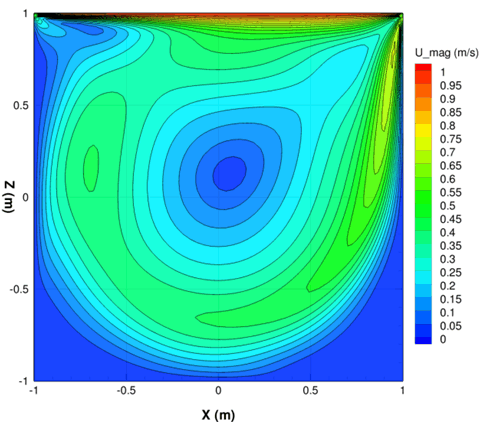
Fig. 3 Velocity distribution in the cavity
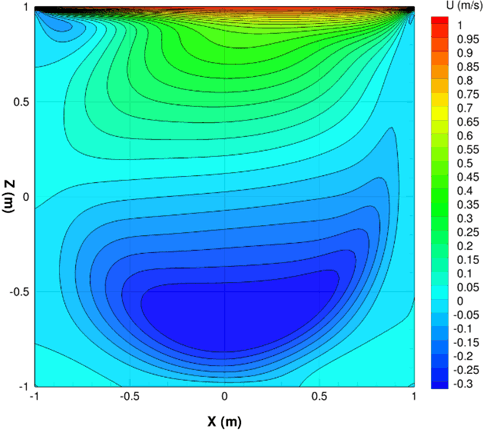
Fig. 4 X-component of the velocity in the lid-driven cavity
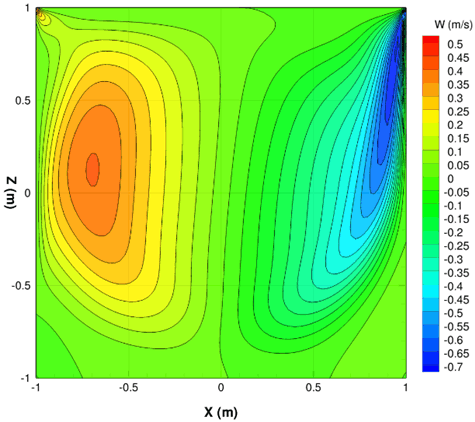
Fig. 5 Z-component of the velocity in the lid-driven cavity
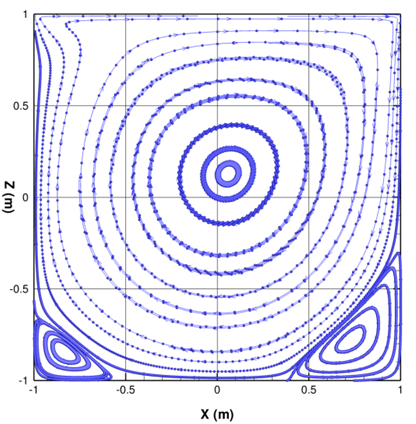
Fig. 6 Streamlines of lid-driven cavity flow
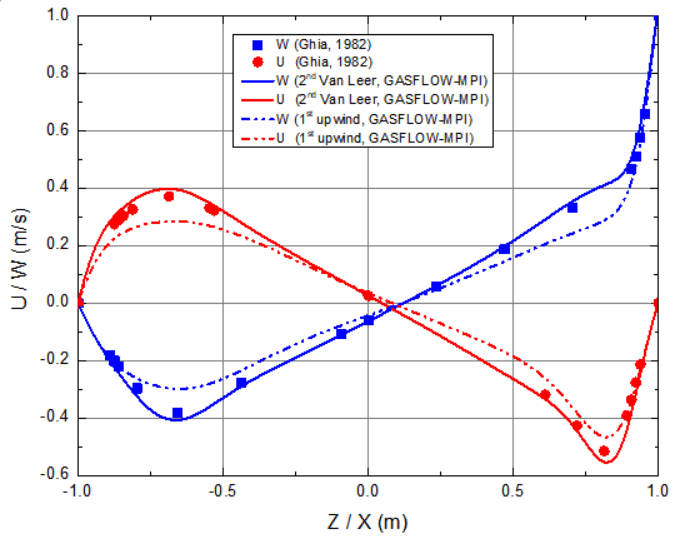
Fig. 7 Velocities along the vertical and horizontal centerlines
Summary
• The second-order scheme is essential for capturing correct flow features in this lid-driven flow case.
• GASFLOW can accurately predict major phenomena in the laminar incompressible shear-driven flow.
Reference
• U. Ghia, High-Re solutions for incompressible flows using the Navier-Stokes equations and a multigrid method, Journal of Computational Physics , 48, 387-411, (1982).
• J. Xiao, W. Breitung, M. Kuznetsov, H. Zhang, J. R. Travis, R. Redlinger, T. Jordan, “GASFLOW-MPI: A new 3-D parallel all-speed CFD code for turbulent dispersion and combustion simulations: Part I: Models, verification and validation”, International Journal of Hydrogen Energy, March 2017.