
Fig. 1 Initial condition for 1-D shock tube
Keywords
Validation, sonic flow, inviscid flow
Purposes
• To simulate the transient flow inside a shock tube using the all-speed solver in GASFLOW.
• To test the stability and resolution of flow discontinuities with the numerical schemes in GASFLOW.
Descriptions
• The Sod shock tube, which can be solved analytically, is a Riemann problem used as a standard test problem in computational hydrodynamics.
• Sod shock tube is widely used to test the accuracy of the CFD codes.
• 1D Euler equation is solved.
• The tube is 10 meters long, and initially filled with stagnant air. The tube is separated into two sections with different pressures and densities, as shown in Fig. 1.

Fig. 1 Initial condition for 1-D shock tube
Testing cases
• Mesh sensitivity analysis is performed using the testing cases below.
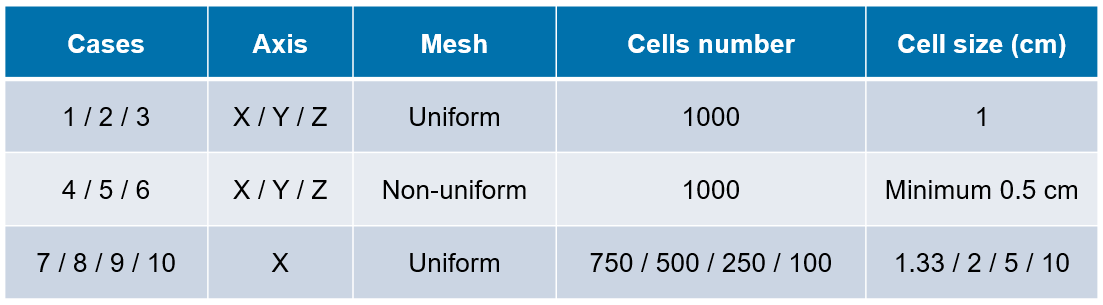
Fig. 2 Testing cases for Sod’s shock tube
Results
• This case shows the capability of the solution algorithm and second order MUSCL differencing scheme utilized in GASFLOW in capturing the unsteady shock and expansion wave motions inside a shock tube.
• When the imaginary membrane is removed at the interface between the high and low pressure section, a shock wave and contact discontinuity propagates into the low pressure region, whilst an expansion fan propagates into the high pressure section. The upstream and downstream ends of the expansion are well resolved, and the contact region is sharp.
• The calculated pressure, density and velocity profiles in 1D shock tube at 0.0061 s are compared to the analytical solutions in Figs. 3~8.
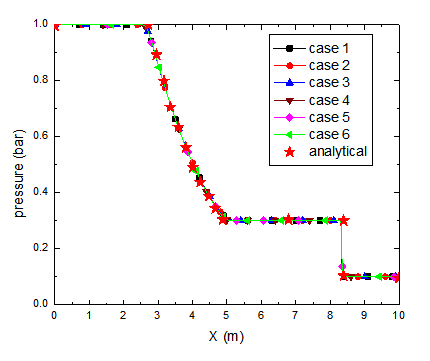
Fig. 3 Static pressure (Cases 1-6)

Fig. 4 Density (Cases 1-6)
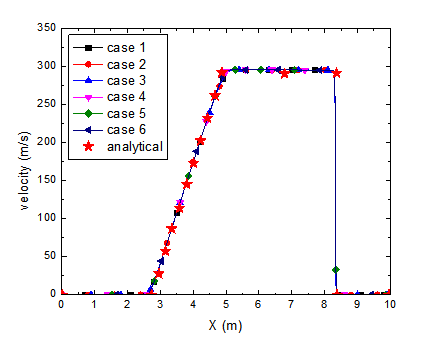
Fig. 5 Velocity (Cases 1-6)
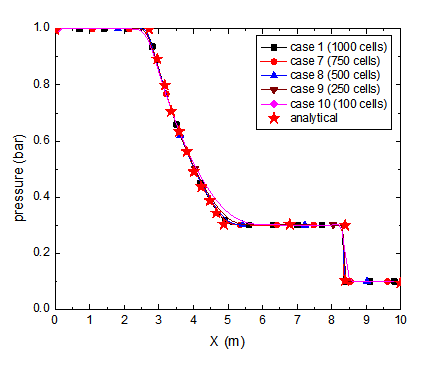
Fig. 6 Static pressure (Cases 7-10)

Fig. 7 Density (Cases 7-10)
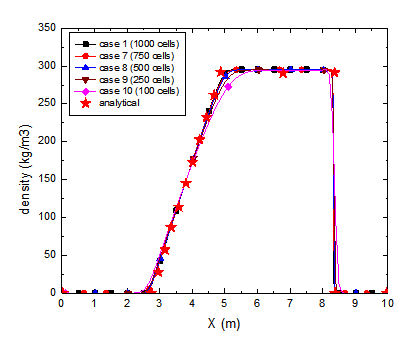
Fig. 8 Velocity (Cases 7-10)
Summary
• GASFLOW was used to simulate the Sod shock tube problem. Very good agreement with the analytical solution was obtained.
• It shows that GASFLOW is capable of modelling compressible flows with strong discontinuities.
Reference
• G.A. Sod, A survey of Several Finite Difference Methods for Systems of Nonlinear Hyperbolic Conservation, Journal of Computational Physics, 1978 vol. 27, pp. 1-31.
• J. Xiao, W. Breitung, M. Kuznetsov, H. Zhang, J. R. Travis, R. Redlinger, T. Jordan, “GASFLOW-MPI: A new 3-D parallel all-speed CFD code for turbulent dispersion and combustion simulations: Part I: Models, verification and validation”, International Journal of Hydrogen Energy, March 2017.